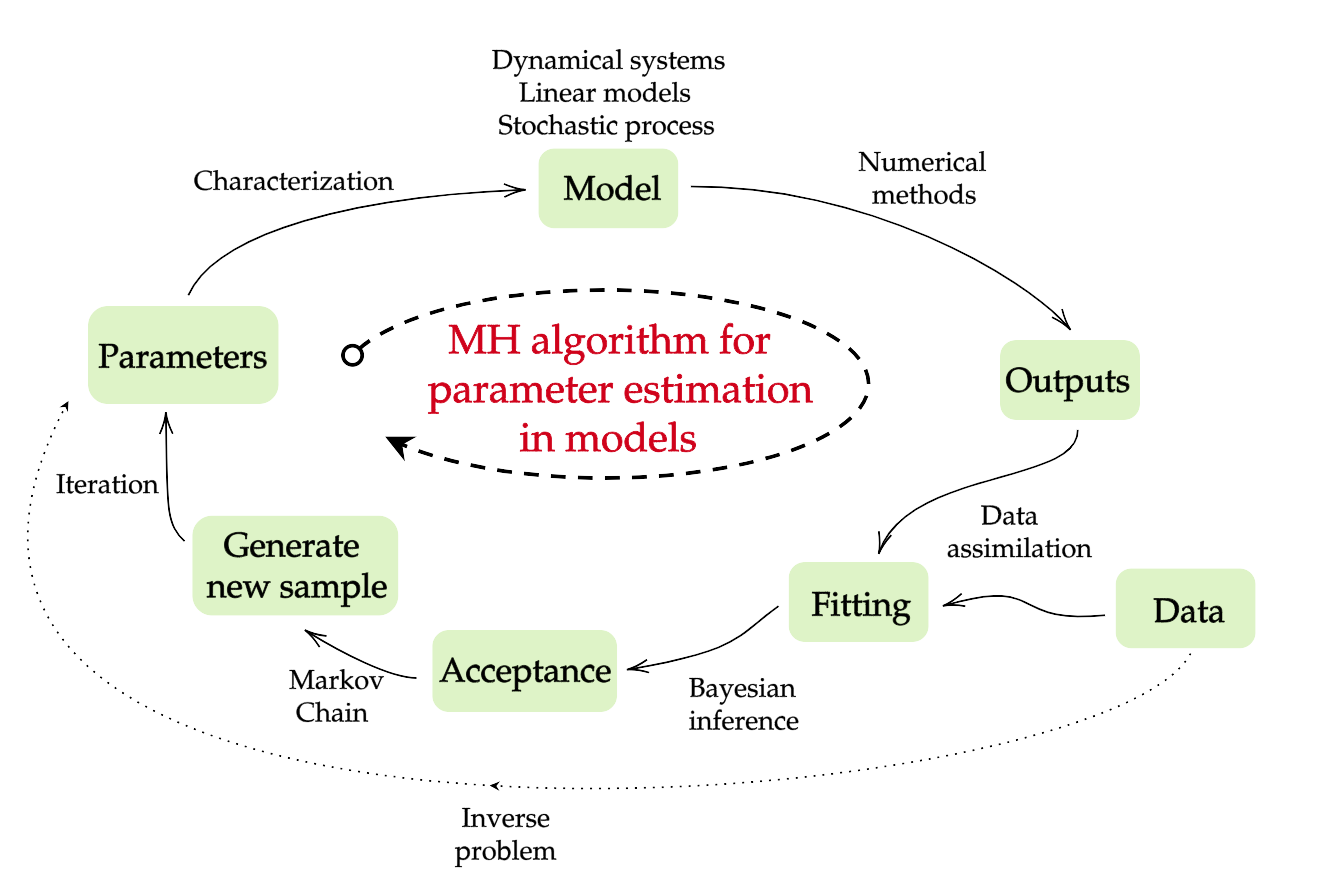
Introduction
Suppose we have information about a measured quantity $y \in \mathbb{R}^{m}$, and with this, we can recover information about another quantity $x \in \mathbb{R}^{n}$. In order to relate these two quantities, we need to know (or construct) a model to understand their dependence. Such a model may be inaccurate and could contain parameters that are not initially known; additionally, the measured quantity $y$ may contain noise. Mathematically,
\[y = f(x,e)\]where $f:\mathbb{R}^{n} \times \mathbb{R}^{k} \to \mathbb{R}^{m}$ is the function representing the model, and $e \in \mathbb{R}^{k}$ is the vector of unknown parameters and noise.
From a Bayesian statistical perspective, all the parameters of the problem are modeled as random variables:
\[Y = f(X,E)\]where $Y, X$, and $E$ are random variables whose probability distributions are related according to the equation above.
Bayesian inference
Markov chain Monte Carlo (MCMC) methods
Metropolis-Hastings (MH) algorithm
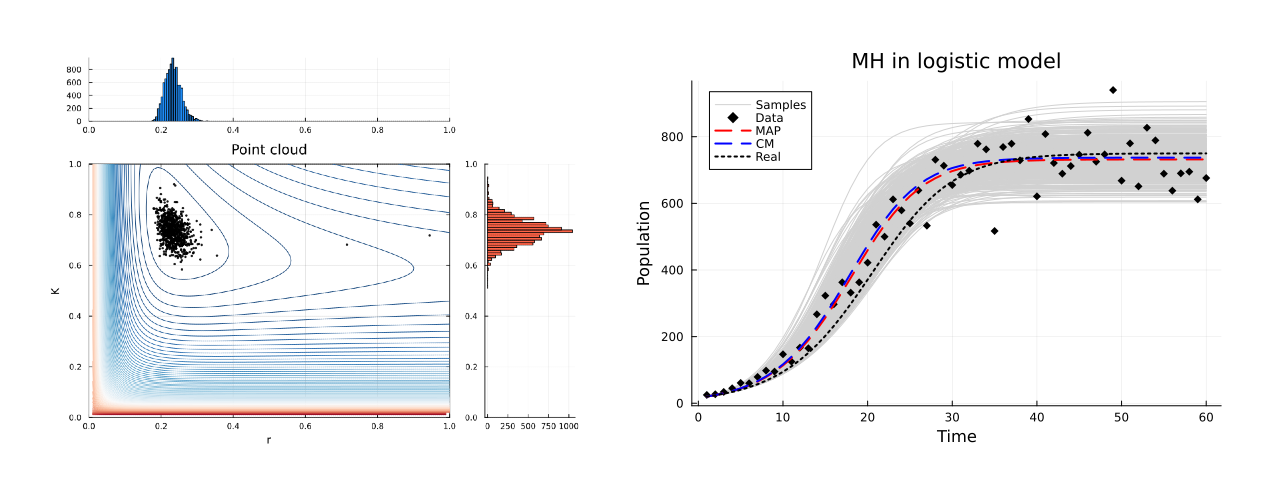
MH algorithm in dynamical systems
References
[1] Galvis, J., & Capistrán, M. (2021). Beyond Research: Asimilación de datos en sistemas complejos [Course].
[2] Kaipio, J., & Somersalo, E. (2005). Statistical and computational inverse problems. Springer
[3] Tierney, L. (1994). Markov chains for exploring posterior distributions. The Annals of Statistics, 22(4). https://doi.org/10.1214/aos/1176325750